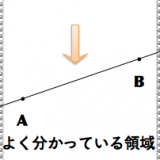
公理2がなければ直線の先がかしゆかの髪の一部ってことだってありえる

手元を照らす公理1に対して、暗黒大陸状態の外側を照らす（それも隅々まで！）のが公理2というのが僕の見解です。

なぜなら･･･

公理1の世界再び

公理1は人類の偉大な第一歩に違いないのですが、所詮は第一歩に過ぎません。

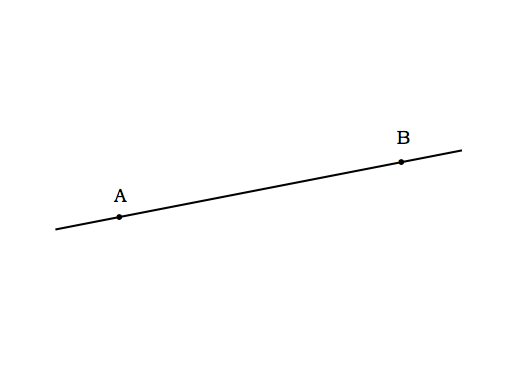
公理1　相異なる二点AとBが与えられたとき、AとBを通る直線をひくことができる。AとBを通る直線はただ一つしかない。

両端が途切れていますけど、要するに誤魔化しているっちゃ誤魔化しているのです。

この事情を分かりやすくしたのが前回提示した以下の図です。

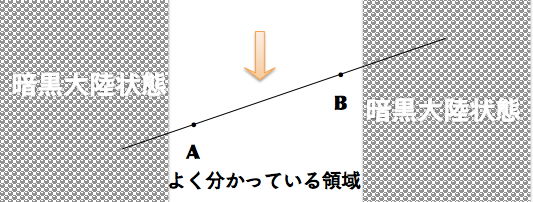
このように、外側の部分について全く何の情報も無いに等しいのです。

だから、もしかすると公理1を説明した図を伸ばしていくと･･･

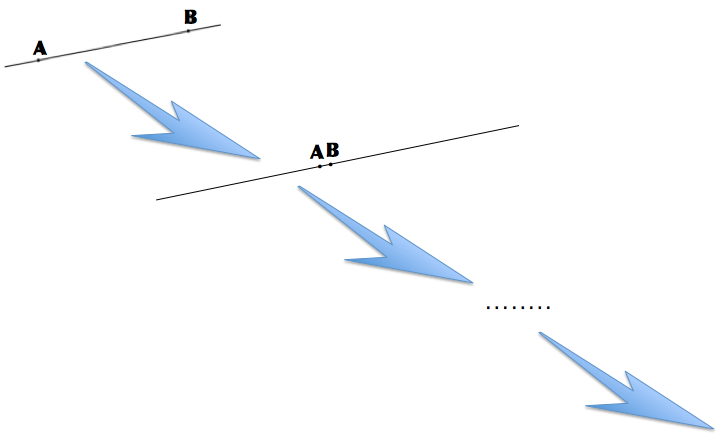
最終的にはこんなことになってるかもしれません。

うはｗ最高ｗ

ところが、こんな幸せな結末ばかりとは限りません。

こう言う場合も無いとは言えないというだけで、そこには無限に近い可能性が残されています。

公理2は、非情にもその無限の可能性をたった一つに固定します。

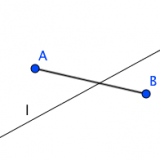
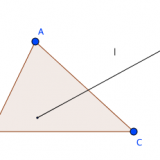
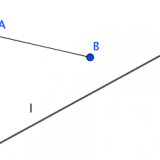
直線lが三点A,B,Cのいずれをも通らないとき、lは三つの線分AB,AC,BCのいずれとも交わらないか、または、そのうち二つと交わって他の一つと交わらない。

詳細は以下の記事参照ですが、この公理2があると直線はどこまで行っても延々と直線であることがハッキリとします。

見事、暗黒大陸状態だった「外」が全て明るみに出て、よく分かっている状態になりました。

破壊力ハンパない。
かしゆかの可能性までなくなってしまったのは非常に残念ですが(^ｰ^;

公理2によって、直線でぶった切られた直線、及びその部分である線分は明確に「こっち」と「あっち」に分けられます。

これはどこまで行こうが直線は途切れることなくずっと続いているから言えることです。

「こっち」と「あっち」（同じ側と反対側）が言えるようになったことで、直線はいよいよその全貌を表すことになります。