去年の7月末、僕は小平先生の『幾何のおもしろさ』に書かれた公理2について記事を書きました。
公理2のメッセージ①:まっすぐ
このとき僕は、公理2が言っていることとして「直線がまっすぐであること」しか読み取れませんでした。
なので、同じく「直線がまっすぐであること」を言っている公理1との区別がつかず、公理1で公理2は証明出来るんじゃないか、とチャレンジしてみました。
そして特別な場合に関しては公理2は公理1で証明出来てしまうため公理とはいえないことを示すところまでは行きました。
その後、全ての場合で公理2を公理1で説明可能かどうかに挑戦したものの、分岐が多すぎて途中放棄、お手上げとなっていました。
しかし今日。
セーラー服のかしゆかとのっちを見ていて、何故か僕は気付きました。
公理2には、「直線がまっすぐであること」以外の情報が入っている。
それは・・・
公理2で除外される可能性
公理2をここに再掲してみます。
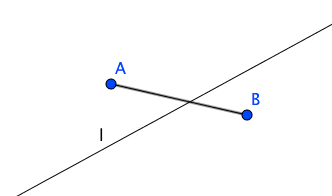
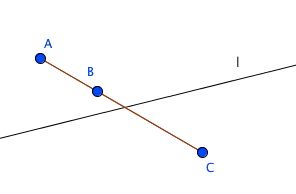
直線lが三点A,B,Cのいずれをも通らないとき、lは三つの線分AB,AC,BCのいずれとも交わらないか、または、そのうち二つと交わって他の一つと交わらない。
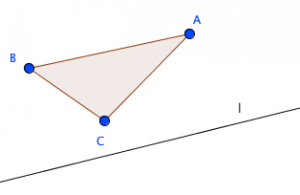
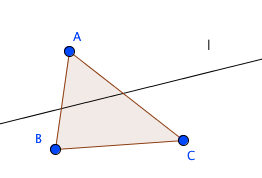
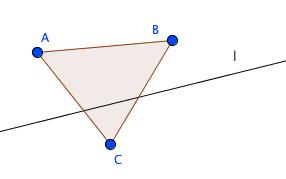
ここで規定されている性質を見ているだけでは気付かなかったことが、ここで除外されているのが何かを考えることで見えてきました。
なんでかしゆかのっちのセーラーでそんなことに気付いたのかは不明です(^ー^;
公理2で除外されるのは次の二つの可能性です。
直線lが三点A,B,Cのいずれをも通らないとき、lは三つの線分AB,AC,BCの
- いずれとも交わる
- そのうち一つと交わって他の二つと交わらない。
このうち、「いずれとも交わる」が除外されるのは、直線がまっすぐだからでしょう。
つまりは公理1のメッセージと同じです。
一方、「一つと交わって他の二つと交わらない」があり得ないのは、直線がまっすぐだからというだけでは言えません。
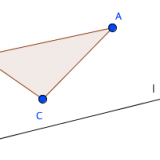
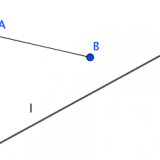
これが起こりうる場面を無理矢理描いてみると、こんな場合が考えられます。
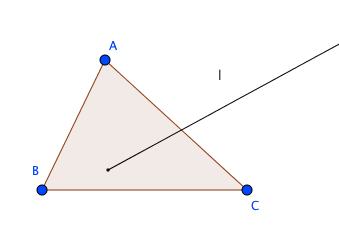
これ、直線じゃないでしょ、と言われてしまうと思いますが、それを保証するのが公理2なのでは。
公理2のメッセージ②:どこまでも続く
つまり、これが起こらないこと、直線はどこまでも延々と続いているという性質は、公理1には含まれず、公理2で初めて保証されるというのが僕の発見です。
どこかに直線の端が存在するのだとしたら、上の図のように、直線と三点ABCが作る線分について、「一つと交わって他の二つと交わらない」がありえることになります。
でも、それは無いと公理2は言っているのです。
これこそが、去年の僕には見えなかった、公理2が公理1とは違っていて、必要であることの根拠です。
直線がまっすぐだということと同じくらい自明に思われる、直線がどこまでも続くという性質は、公理2によって説明されているということです。