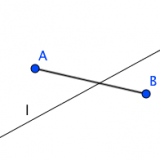
公理2は公理1と同じく、直線がまっすぐであることを言っているように思えたのですが・・・
公理2
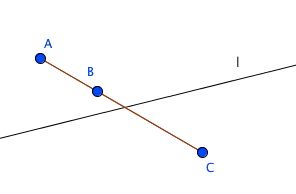
直線lが三点A,B,Cのいずれをも通らないとき、lは三つの線分AB,AC,BCのいずれとも交わらないか、または、そのうち二つと交わって他の一つと交わらない。
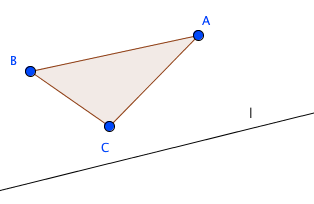
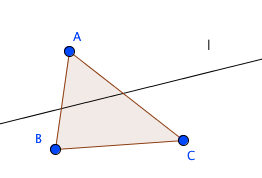
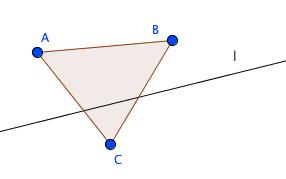
図は小平先生の『幾何のおもしろさ』に書いてあったものを模して作りました。
この前のところで、線分を直線の一部として「端点プラス間の部分」というように定めています(が、何故かこれは「定義」としては扱っていません)。
公理2は直線が真っ直ぐでないと成り立ちません。
そこで、公理2が直線の真っ直ぐさを表すものだと考えるべきだと思うのですが、ちょっと引っかかります。
というのも、まさに公理1も直線が真っ直ぐであることを言っているのだと僕は考えたからです。
同じことなら敢えて別の公理にする必要はないはず・・・そこで、公理1から公理2は証明できないかを考えました。
三点の並び方
直線l上にない、相異なる三点A,B,Cが存在するとします。
公理1より、相異なる二点を通る直線がただ一つ定まりますから、少なくとも二点は同じ直線上にあります。
公理1
相異なる二点AとBが与えられたとき、AとBを通る直線をひくことができる。
AとBを通る直線はただ一つしかない。
もう一点は、二点により定まった直線の上にあるか、直線の上にはないか、です。
よってこの三点は、全て同じ直線上にあるか、二点が同じ直線上にあって、もう一点は直線の外にあるかのどちらかです。
そこで、
- 三点が全て同じ直線上にある場合
- 二点が同じ直線上にありもう一点はその直線の外にある場合
の二つに分けて考えます。
三点が全て同じ直線上にある場合
では、Ⅰの場合についてです。
このとき、三点A,B,Cは全て同じ直線の上にあり、三点がA、B、Cの順に並んでいるものとします。
二つの線分AB、BCは線分ACと重なっています。
よって、直線lが線分ACと交わるならば、同時に線分ABかBCとも交わることになります・・・☆
点A,B,Cを通る直線を直線mとすると、公理2の条件より点A,B,Cは直線l上にはないので直線mとlは同じ直線ではなく、相異なる二直線です。
よって、定理1より直線mとlは交わらないか、ただ一つの点で交わるかのいずれかです。
定理1
相異なる二直線は交わらないか、またはただ一つの点で交わる
Ⅰーa)交わらない場合、mの部分である線分AB、AC、BCとも直線lは交わりません。
Ⅰーb)交わる場合、その点をPとします。
点Pは直線l上の点なので、点A,B,Cと重なることはありません。
よって、点Pは線分ACの間にあるか、外にあるかのいずれかです。
点Pが線分ACの間にある場合、直線lは線分ACと交わることになりますが、☆よりこの場合は同時に線分ABかBCとも交わることになります。
なので、点Pが線分ACの間にある場合、直線lは線分AB,AC,BCのうち二つと交わって他の一つと交わりません。
また、点Pが線分ACの外にある場合、直線lは線分AB,AC,BCのいずれとも交わりません。
以上、Ⅰーaおよびbより、三点が一直線上にある場合は公理1から公理2は導けます。
つまり、この場合に限っては公理2は公理ではなくて定理です。
三点が同じ直線上にない場合
一方、三点が同じ直線上にない場合Ⅱを考えます。
このとき、直線AB、AC、BCは全て相異なる直線です。
線分は直線の部分なので、取りあえずは線分ではなく直線で考えてみます(直線なら公理1、定理1が使えるからです)。
すると、定理1より直線AB、AC、BCと直線lの間にはそれぞれ「交わる」か「交わらない」のどちらか二通りの可能性があるため、次のように8通りの関係が考えられます。
- 直線lは直線AB、AC、BCそれぞれと交わる・・・1通り
- 直線lは直線AB、AC、BCのうち二つと交わって他の一つと交わらない・・・3通り(交わらない一本の選び方が三通りある)
- 直線lは直線AB、AC、BCのうち一つと交わって他の二つと交わらない・・・3通り(交わる一本の選び方が三通りある)
- 直線lは直線AB、AC、BCのいずれとも交わらない・・・1通り
直線を線分にした場合、交点の数は減るか、そのままかのどちらかです。
よって可能性としては・・・
もうやだ(^ー^;
公理2はこのように超面倒くさいたくさんの可能性を局限まで絞るものなのだということが分かりました。
それで充分です。
2017年追記
いやいや、十分じゃありません(^ー^;
もっと面白いことに一年越しで気付きましたよ。