小平幾何の続きです。
公理2によって、「直線はまっすぐ」なだけではなく「どこまでも続く」ということが分かりました。
そこで出てくるのが、定義1です。
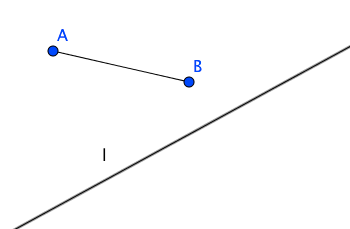
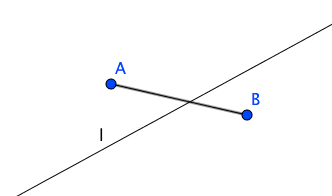
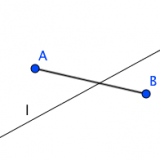
線分ABが直線lと交わらないならば、点AとBは直線lの同じ側にある。線分ABがlと交わるならばAとBは直線lの反対側にある。
これは交わらない、交わるを別の言葉で言い換えているだけなのですが・・・
そんなことが可能になるのは、公理2で追加された「直線はどこまでも続く」という事情があるからこそ、です。
どこもまでも続くから、同じ側、反対側、といった領域の区別による表現が出てくるのも自然な流れ。
よし。
これで、まどろっこしかった公理2の導く世界が視界明瞭になってきた・・・はず。