公理2によって、直線はどこまでも延々と続く性質を持つことが示されていることに先日気付きました。
この気づきによってその後の展開が非常に見通し良くなったのですが、「どこまでも続く」というのが公理2のメッセージだというのは、ちょっと舌っ足らずな表現でした。
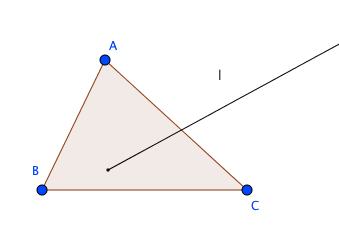
上の図のような事態は公理2の元ではありえないので、直線には端は存在しません。
でもそれだけでは不十分で、より正確を期すためにさらに表現を追加します。
直線は、端がないだけでなく、途中で途切れることもない、というふうに。
途切れがあるなら、端が存在すると仮定した場合と同様に、公理2で除外されている最初の図のような状況が発生してしまいます。
よって、直線に途切れはありえません。
ここで、もう1度公理2を掲げます。
直線lが三点A,B,Cのいずれをも通らないとき、lは三つの線分AB,AC,BCのいずれとも交わらないか、または、そのうち二つと交わって他の一つと交わらない。
この味も素っ気もない公理2ですが、そのコアなメッセージは、直線はまっすぐで、なおかつどこまでも途切れなく永遠に続く、というものです。
言い方は無愛想極まりないですが、どんな表現よりも雄弁に強固に確実に、絶対的に直線が途切れることなくどこまでも延びていることを宣誓しています。
なんか…
これって数学なはずなんですけど、まるで詩のような味わいがあります。
そしてこの後に続く、公理2が導く定理により更なる旅情豊かな世界が待ち受けています。
世界中のどこにも絶対に存在しえないような、人間の内面にしか存在しない独自の平野が広がっていきます。
なんて愛おしいんだろう、この公理2ってやつは。