手元を照らすのが公理1

『幾何のおもしろさ』での公理1、2はどっちも直線の性質を規定していますが、あえて違いを強調してみるのなら公理1は手元を照らすものだと思います。

2点A,Bの間

公理1は以下。

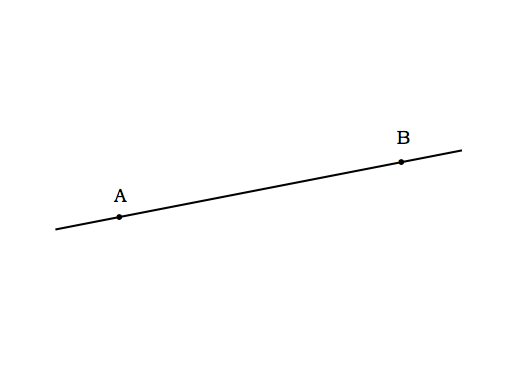
公理1　相異なる二点AとBが与えられたとき、AとBを通る直線をひくことができる。AとBを通る直線はただ一つしかない。

この図は『幾何のおもしろさ』にあったのと同じです。

で、この図こそが公理1の特徴そのものです。

2点A,Bの間と外があって、間はハッキリしているけれども、外はよく分からない･･･いわば暗黒大陸状態です。

2点A,Bの距離はもしかするともの凄く開いてるかも知れないんですけど、とにかくこの2点の間は認識の範囲内に収まっています。

一方、外に関しては一応同じような直線が続いているはずではあるものの、実際のところ公理1からだけではよく分からないというのが正直なところではないでしょうか。

公理1の枠内では半直線は議論されません。

線分の定義のみが行われます。

線分ABとは、直線AB上の、AとBの間にある部分と、点A、点Bを加えたもの

これは公理1だけで説明可能です。

ところが、外までを範疇とする半直線は、公理2を持ち出してから議論されます。

逆に言えば、公理1だけでは扱いにくいのです。

また、『幾何のおもしろさ』では煩雑を避けるためにすっ飛ばされている、直線上の第三の点の位置に関する説明でも、間はハッキリしているが外はよく分からないという背景が透けて見えます。

直線上にはA、B以外に第三の点が存在することが、そのすっ飛ばされた公理で規定されるのですが、その位置を以下のように説明しています。

二点AとBを通る直線AB上にAともBとも異なる点Cをとれば、CがAとBの間にあるか、AがCとBの間にあるか、BがAとCの間にあるか、のいずれかである。

すごくまどろっこしいですけど、図にすると簡単。

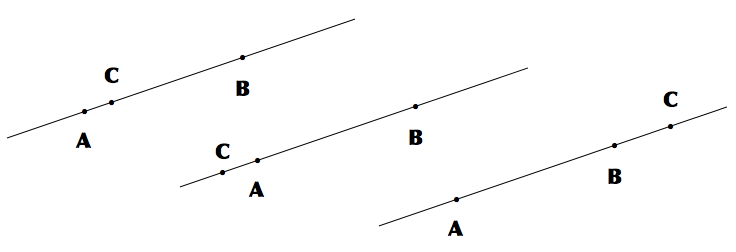
第三の点Cは、二点AとBの間か、A側の外か、B側の外だと言っているだけの話です。

以下に矢印で示したように、AともBとも異なって直線上にあるのであれば、この3つのゾーンのどこかにあることは明らかです。

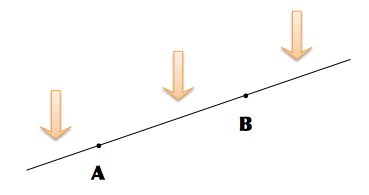
が、公理1しかない状態では、この矢印3本で示したゾーンの明らかさはちょっとグラデーションがあるのだと思います。

以上二つの事例から考えるに、公理1しかない世界では、二点の間ははっきりしているけど、外はよく分からないのです。

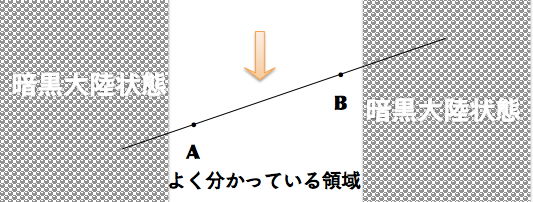
なので、線分は定義したとしても半直線は議論しない方が良く、第三の点の位置が3箇所あることを言うのにいちいち挟む二点を使って説明しているのだと思います。

なんでこんな事態になったのでしょうか？

それは、人間が世界を認識するときには、まずは区切られた手元から始める仕方が自然だからなのだと思います。

ユークリッドもヒルベルトも、結局は大差ないこの公理1と同様の公理から始めています。

そしてその次に、今度は外の世界へと視界を広げていくのだと思います。

そんなわけで、次なる公理はこの外の世界を定めるもののはずなのですが、そう単純には進みません。

それが、上で議論した第三の点の存在を規定する公理の必要性です。

第三の点は直線上にも直線の外にもあって、それぞれ公理が必要なのですが･･･

小平先生は、それをやり始めると超複雑な順序の議論をしなきゃいけなくなるからということで、フォントを小さくして意欲のある人だけ読めば良いように別枠扱いにしています。

で、とっとと公理2、外側を定める議論を開始します。

超親切(^ｰ^)

タイトルが「おもしろさ」となっているのも納得の展開です。

というわけで、次は公理2で世界がどう変わるかを確認して（といっても既に議論済み何ですけどｗ）、半直線の定義を見てみます。