今日はなんてことのない平面幾何の証明を、ちょっとずるい手を使ってやってみます(^ー^;
問題のおさらい
問題については前回、前々回の記事を参照ください。
今回は残る問題である以下の証明に取り組みます。
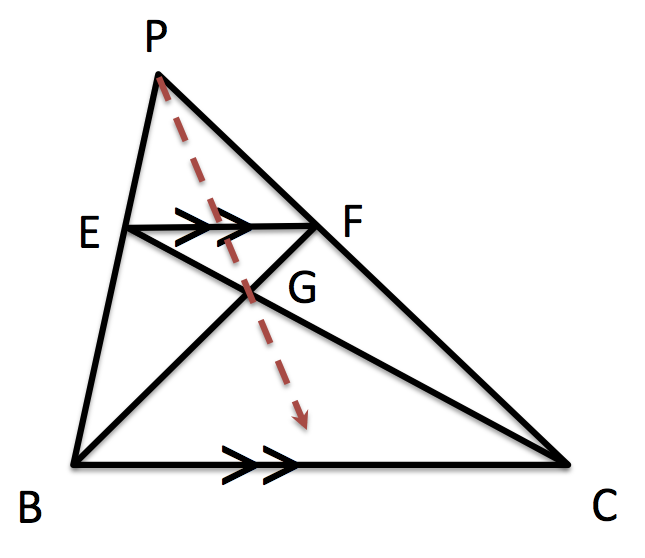
三角形PBCについて、辺PB上に点E、辺PC上に点FをEFとBCが平行になるようにとり、EC、FBの交点をGとする。
このとき直線PGは辺BCの中点でBCと交わる。
ここで、僕は真っ先に上のかしゆかが思い浮かびました(^ー^;

美しい(*´д`*)
なんてことはさておき、僕はこの問題と「逆」の問題をやったことがあってそれを思い出しました。
逆の証明
これは「高校への数学」シリーズの別冊「解法のスーパーテクニック」に出ていた問題です。
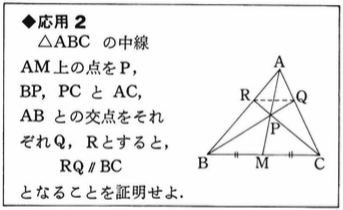
解答は二つ示されていて、どちらも補助線のテクニック「外の空間を使え」が用いられています。
僕が使えそうだと思ったのは、以下のように補助線を引くやり方です(『解法のスーパーテクニック』より)。
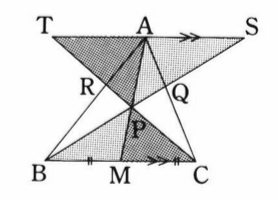
Aを通るBCに平行な直線を引き、BP、CPとの交点をそれぞれS,Tとしたのが上の図です。
証明の続きは是非とも『解法のスーパーテクニック』をお読みください。中学生向けですけど、趣味でやるには十分難しくオススメです。
この補助線をパクれば、今回の証明も出来ます。
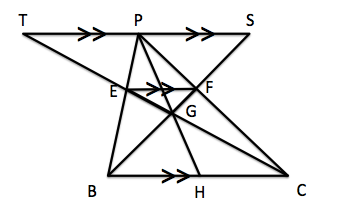
パクリの補助線を引いて、PGとBCの交点をHと置きます。
分かってるのは、
TS‖EF‖BC・・・☆
のみ。HがBC上のどこにあるかは分かりません。
この状態から一瞬・・・いえ、二瞬で片付きます(^ー^)
TP=PS
まずはこの図でTP=PSとなっていることを示します。
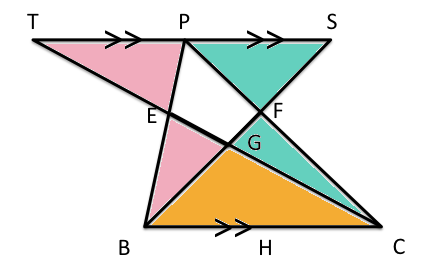
☆から、TS‖BCなので、△EPTと△EBC、△FPSと△FCBがそれぞれ相似となります。
よってTP:CB=PE:EB・・・①、PS:CB=PF:FC・・・②
また、同じく☆よりEF‖BCなので、
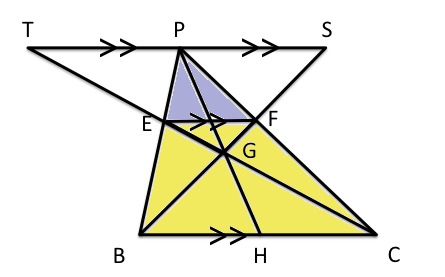
PE:EB=PF:FC・・・③。
①、②の右辺は③により等しい比なので、TP:CB=PS:CB。
比の値を取ると、CB×TP=PS×CBで、CBはゼロではないので両辺をCBで割るとTP=PS・・・★。
楽勝です(^ー^)
BH=HC
ではいよいよラスト。
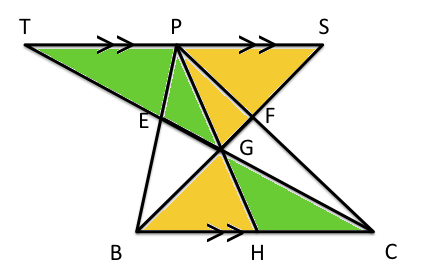
☆より、TS‖BCなので、TP:HC=PG:GH・・・④、PS:BH=PG:GH・・・⑤。
④と⑤の右辺は同じなので、まとめてTP:HC=PS:BHですが、★よりTPとPSは同じ値なので、比の値をとればBH=HC。
よって、HはBCの中点(証明終わり)
余談
このようにしてSEGの中1向け問題の一部が解けました(^ー^;
中1(^ー^;
どうも本当にすいません、としか言いようがないくらいSEGってぶっ飛んでるなーと思いました。
一番面白いのは、何といっても自由に点を置いて良いということに気付くところだと思います。
僕はこれに気付くのに数日を要したわけですが、それは中途半端に問題をパターン化(対角線を引く、など)に当てはめて対処しようとする下心があったために自由な発想が出来なかったからだと思います。
僕の中途半端さはしかし、恐らくは教育によりたたき込まれたものです。
数学ってのは教科書に書いてあるやり方でやってくんだよ、みたいな。
素材を元に好き勝手自由に色々試してみるもんだ的な発想は欠けていました。
そんなわけでこれを数学を学び始める中1でやらせるというのは、とてもよい教育だと思います。
少なくとも、オマケやらアプリやらで消費者心理をくすぐるしか能のないベネッセなんかよりはずっと本気の「教育への熱意」を感じます。
うちの子はまだまだ小さいんですけど、親としてこういう教育する側の人たちの熱意の違いは判断できる大人でいたいですね!
そしてかしゆかはすごくかわいい(*´д`*)
Perfume First Tour『GAME』 [Blu-ray]







