進学塾のSEGが中1向けに公開している問題を一つ、一週間かけて解きました!(^ー^;
平面幾何の面白さに触れる
SEGといえば、東大目指しているような人が通うすごく難しいことをやっている塾という印象です。
今更進学塾なんて無縁な僕ですけど、地味に趣味が数学なので数学教育に気合いを入れているSEGが気になってサイトを見てみました。
- 参照サイト:科学的教育グループSEG
そこで中1向けの公開問題を見つけました。
平行四辺形が書いてあって、(1)、(2)と二題出題されています。
このうち最初の一題を一週間かけて解きました(^ー^;
結構面白かったので記事にしてみたいと思います。
ちなみにSEGの商売を妨害するつもりは全くありませんので、(2)以降に関しては一切触れないようにします。
あまりにも面白かったので(1)だけ僕の回答プロセスを述べさせていただければと思います。
対角線以外の直線が見えない(^ー^;
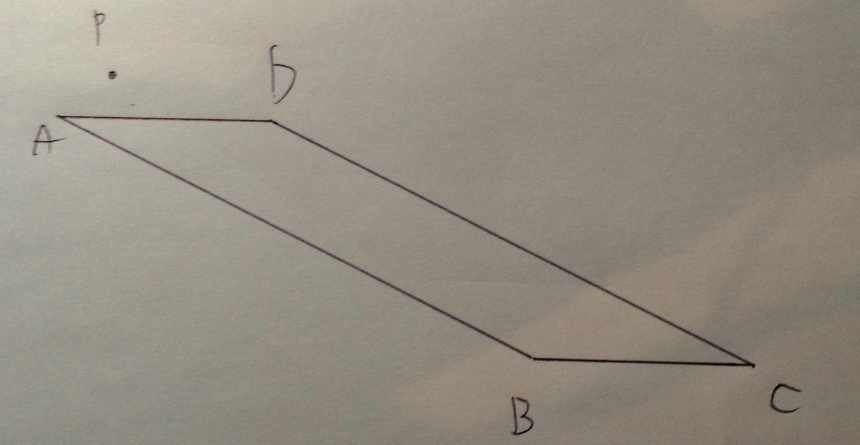
【問題】平行四辺形ABCDがある。
(1)BCの中点Mを定規(2点を通る直線を引くことしかできない)だけで作図する方法を考え、それが正しいことを証明せよ。
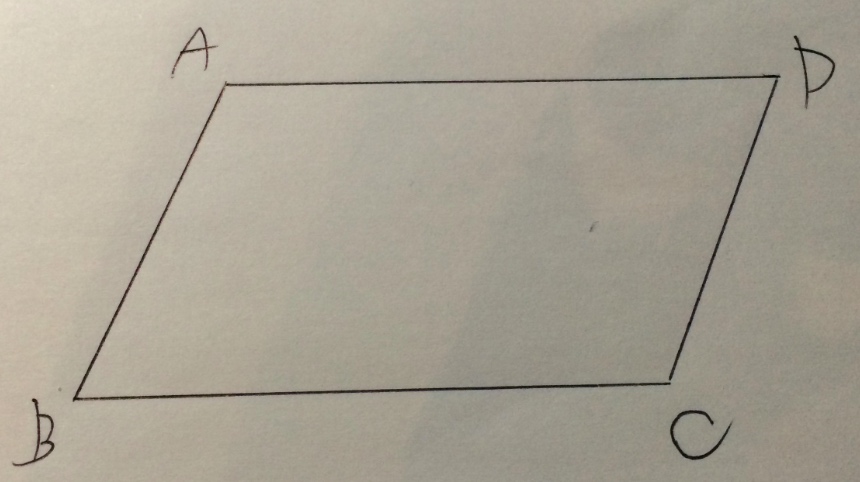
図形が斜めっててすんません(^ー^;
これ、まずは対角線を引くのかな、と思いますよね?
でもそれだとその先がうまくいかない、と書いてあります。
じゃあ別の線を引かなきゃいけないわけですけど・・・え、他に引ける?ってのが僕の最初の感想でした。
二点を通る直線を引くことしかできなくて、図で「点」は平行四辺形の4つの頂点だけですから、対角線がダメなら各辺を延長するしかないけれども、そんなことしたって到底中点Mは作図できそうにはありません。
わかんねー(^ー^;
で、諦めました。
でも四日後。
仕事を終えて帰宅して、ベッドに入った瞬間、突如直線が・・・というよりは、「点」が見えてきました。
こういう瞬間が楽しくて、僕は数学を趣味にしてるんですよ!
直線上に無い点を置いていい
平行四辺形の4頂点以外に点は無い、と僕は思っていましたが、そんなもの自由に置いてしまえばよかったのです。
どこでもいいから(^ー^)
そんなことしちゃダメなんてどこにも書いていません。
そこで僕は、平行四辺形のちょっと上に、ためらいがちに、そっと点を置いてみました。
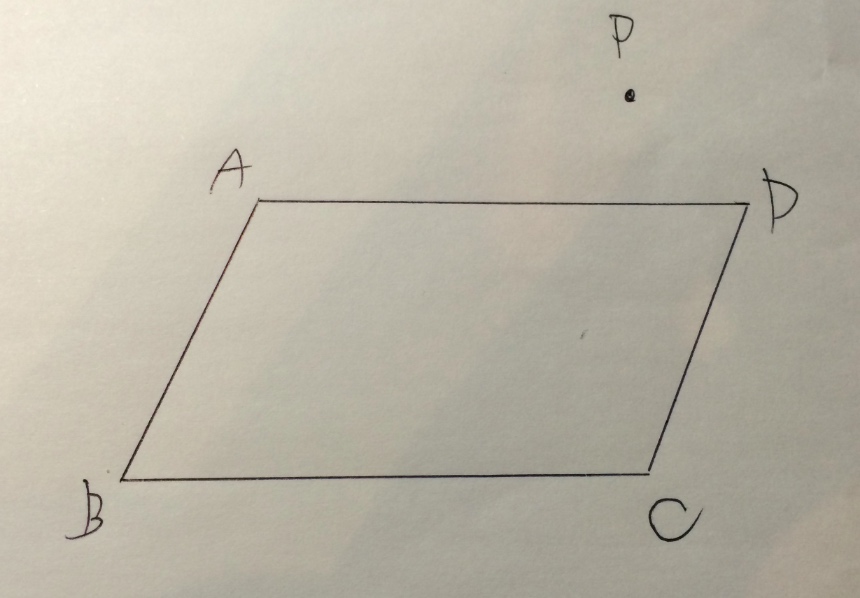
この点Pとなら、状況を打開する直線が引けそうです。
取りあえず、交点が出てくるB、Cとの直線を引いてみました。
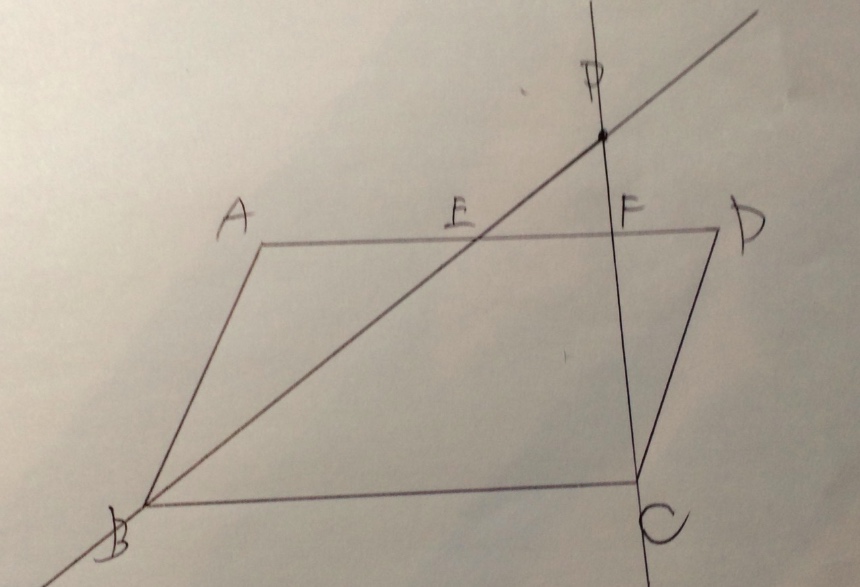
おお、交点が二つ現れました(^ー^)
Aに近い方からE,Fと命名してます。これを使ってまた直線が引けますので引いてみます。
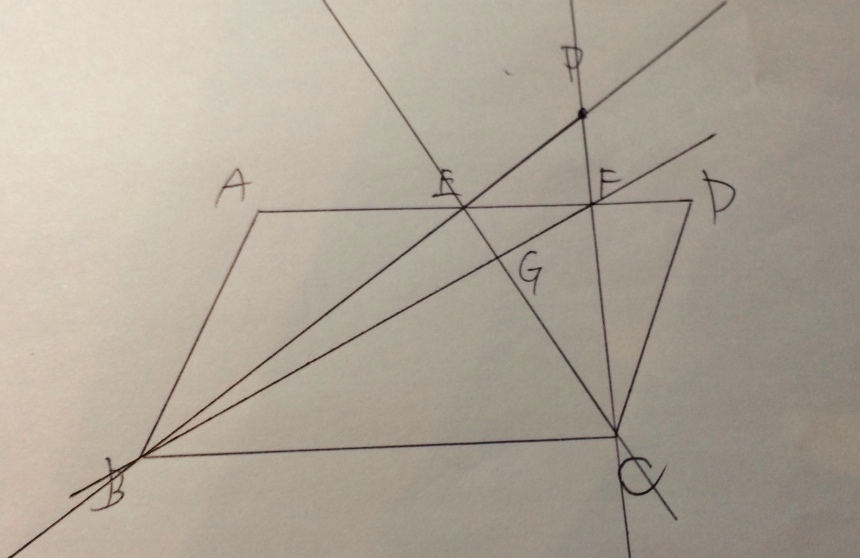
するとまた交点Gができました。
この調子でいくらでも点を増やすことができそうです(^ー^)
引けるだけ直線を引いてみるのも面白そうですけど、目的は辺BCの中点Mですから、BCの真ん中あたりを通りそうな直線は引けないか、と見ていると・・・
PとGを結ぶ直線がそれっぽいですよね(^ー^)
早速引いてみました。
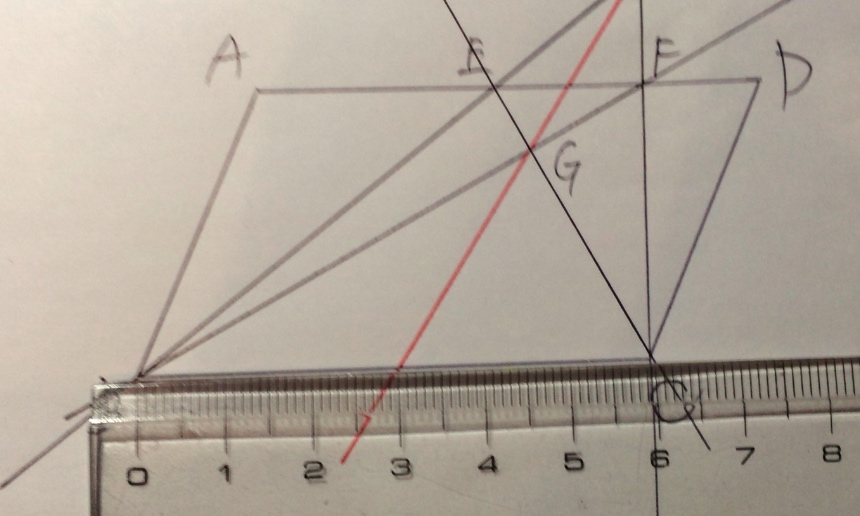
問題文には定規で長さを測って良いとは書いていませんが、勝手に計ってみました。
かなり正確にBCの中点Mを通っているように見えます。
でも、最初に適当に置いたPがたまたま絶妙なポジションだったってことも考えられます。
そこで最初の点の位置をずらして、点Pとは別の点P’を作ってみました。
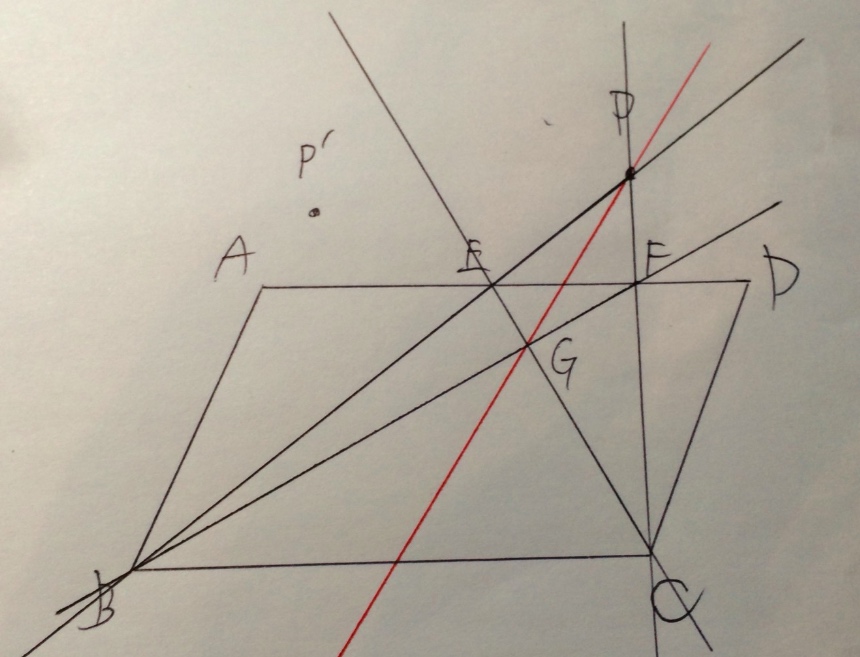
これに対してさっきと同じように直線を書いていってG’を作図してみます・・・
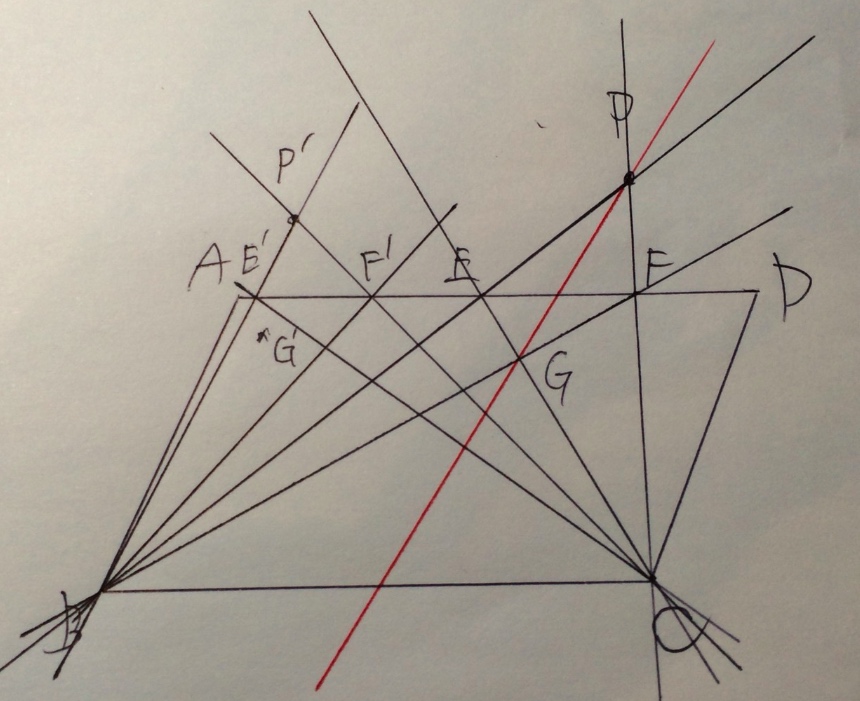
で、P’とG’を結ぶ直線が、さっきのPとGを結ぶ直線と辺BCとの交点らへんを通ればいいのですが・・・
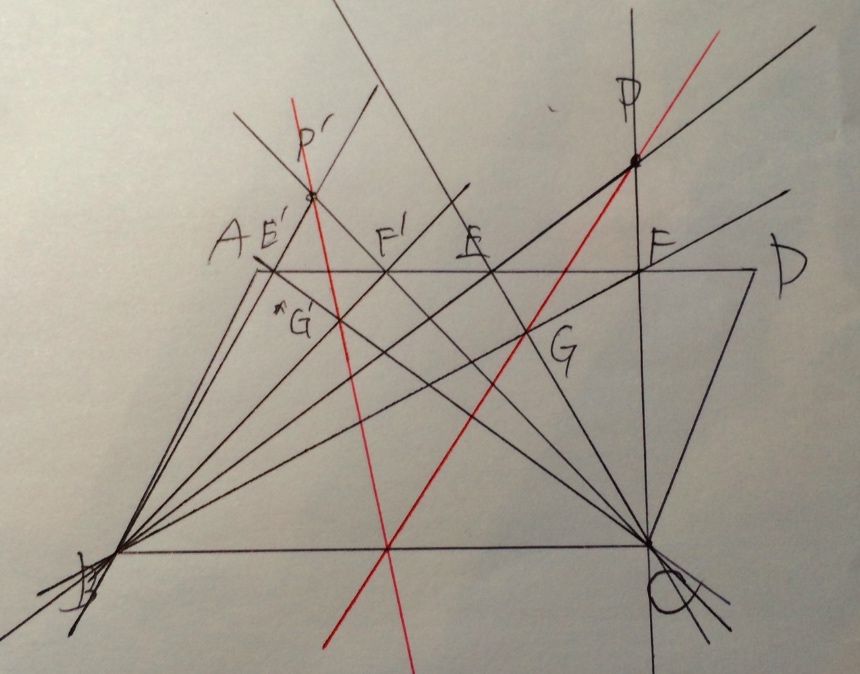
面白っ!!!!
見事に同じところを通りました。テキトーにとった二点PとP’でこのように全く同じ点(しかも恐らくは中点)を通る直線が引けるなんて、まさに神の見えざる手を感じてしまう瞬間です。
たぶん作図法はこれで間違いないはずですが、一応平行四辺形の形を変えてもやってみました。
どんな平行四辺形でも成り立たないといけないわけですから、最初に作った平行四辺形がたまたま都合の良い形だったってこともありえます。
レザビの決めポーズ(ストレイト〜♪)みたいな平行四辺形です(^ー^)
さっきと同じように外側に点Pを取りました。
で、ガシガシ直線を引いていって、E,F,Gと作図していきます。
PとGを結ぶ直線を引いてみると・・・
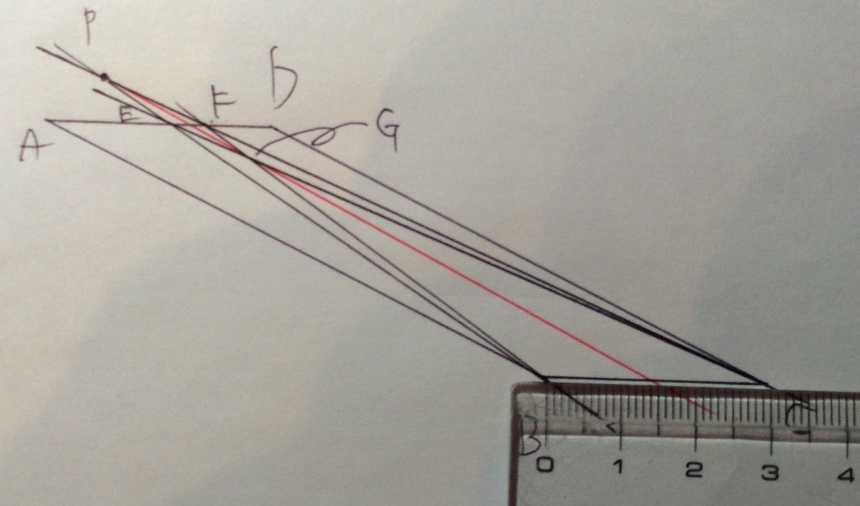
やっぱり中点を通っている!!!!
平面幾何というとただの暗記なイメージが強いですけど、こういう体験をすると数学の法則性のすごさを体感できてかなり楽しいですね。
舞台は平行四辺形から三角形へ
次にするべきことは、このやり方で「中点が作図できる」ことの証明です。
これはどうやら平行四辺形の問題と言うよりは、三角形と平行線の問題であるような感じです。
僕はこの証明に3日を要しました(^ー^;
そこで、次の記事でやってみようと思います。
証明の方も面白かったんですけど、何と言っても今回の記事で書いた「自由に点を置ける」ことに気付いた瞬間が一番面白かったです(^ー^)




