平行四辺形の辺の中点を定規だけで作図するという、SEGの中学生向け公開問題に30過ぎのおっさんが挑戦する第二弾です(^ー^)
問題のおさらい
この記事は以前取り組んだものの続編です。前回の記事はこちら。
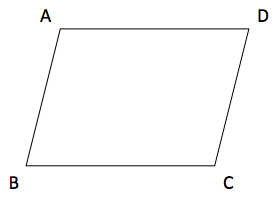
【問題】平行四辺形ABCDがある。
(1)BCの中点Mを定規(2点を通る直線を引くことしかできない)だけで作図する方法を考え、それが正しいことを証明せよ。
前回は問題の前半部分、「作図する方法を考え」のところまでチャレンジしてみました。
今回は次のステップ、証明にうつりたいのですが、そのためにまずは「どう証明するか」の前に「何を証明するか」を考えます。
問題解決の糸口
平行四辺形ABCDの外に適当に置いた点P。
これがこの問題の解決を導く最初の一手でした。
点Pから頂点B、Cとを結んで直線を引くと辺ADとの交点E、Fが出来ます。
点Eと頂点C、点Fと頂点Bとを結ぶ直線を引くと交点Gが出来ます。
点Pと点Gを結ぶ直線を引き、辺BCとの交点の位置を調べてみると・・・なんとBCの交点になっていました。

このように点Pがうまく置ければ後はひたすら定規で線を引いていくだけですので、最初の点Pの位置がどこにあればいいか、を考えました。
点Pの条件
適当に置いた点Pですが、どこでもいいというわけではありません。
もともとこの点Pは問題文にある「2点を通る直線を引くことができる」という” 定規の条件”を利用するために置いたものでした。
点Pが無い状態では、定規を使って出来ることは各辺の延長か、対角線を引くことだけです。
なんとなく対角線を引けばいい気がしましたが、SEGから「対角線を引いてもうまくいかない」とのコメントがありました。
では点Pはどんな点であればいいかというと、点Pと頂点B、Cを結ぶ直線が、辺ADと交わり交点E、Fが出来る。
そんな点PならOKです。
そこで考えついた点Pの条件は、
- 条件:点Pは辺ADに対して、辺BCがある側とは反対側にある。
です(下図参照)。
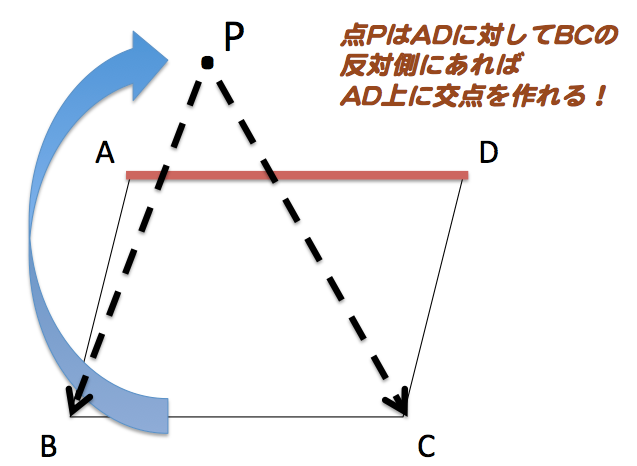
これなら交点E、Fが出来るだろうと思ったのですが・・・
「辺ADに対して反対側」というのがちょっと曖昧に思えました。
辺ADは点A、Dで切れてしまっていますので、その左右の領域がどっち側か分かりにくいです(下図参照)。

そこで直線ADを想定して、それに対して辺BCの反対側、と言った方がより明確にどっちの側かが言えます。
直線は平面を2つに分割するので曖昧なゾーンが無くなります。
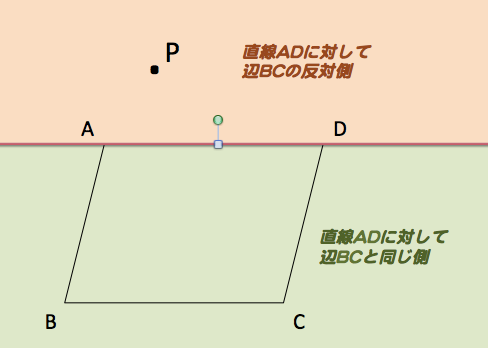
そこで、条件を次のように設定しなおしました。
- 条件:点Pは直線ADに対して、辺BCがある側とは反対側にある。
条件としては分かりやすくなったと思いますが、交点E、Fが辺ADではなく、直線ADとの交点に拡張されてしまいます。
が、結局それでも問題ないことが作図をしてみれば推測されるので結果オーライです(^ー^)

一番大事な点Pの条件が決まったので、次はこの条件で証明すべき問題はなんだったかを考えてみます。
三角形と平行線
辺ADは直線ADと考えて問題なかったので、点A、Dの位置は特に気にしなくてよさそうです(辺BCと平行な直線が必要なだけです)。
むしろ、PB、PCとの交点であるE、Fが作図では使用されました。
ということは、平行四辺形ABCDで証明する必要はなく、もっと簡略化した図形、三角形PBCで証明を試みれば良さそうです。
以下の様な三角形を想定します。
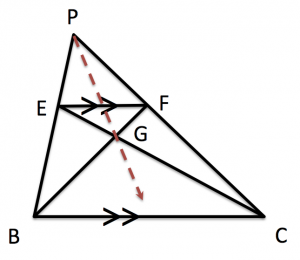
三角形PBCがあって、辺PB上に点E、辺PC上に点FをEFとBCが平行になるようにとり、EC、FBの交点をGとします。
このとき直線PGが辺BCの中点を通る。
これが今回証明すべき命題です。
平行四辺形が消えて、三角形と平行線の問題に早変わりです。
アタマの中にはPerfumeのアルバム、トライアングルのイントロ「take off」が流れ出すところです。
これなら中学数学の平面幾何で普通に出てきそうな問題です。
が・・・(^ー^;
次回、やっとこさ証明をしてみます(^ー^)
中学生がやる問題を、数週間かけて解決してみるという悲惨な記事笑は、いよいよ次回最終回です。