『メノン』における想起説は「知識」を思い出すのではなく「理性」を思い出すのだという予想が間違っていないことを、ソクラテスが示す想起説の実例を見て確認します。
とはいえ、この実例、何がどう想起説の実例になっているのか僕にはよく分かりにくいものでした。内容的には中学レベルの数学ですので決して理解しにくいものではないのですが・・・
ひとまず今回は、『メノン』の想起説の実例で何が行われたかを確認することで一杯一杯です(^ー^;
正方形の面積の問題
メノンくんはソクラテスの言う想起説が信じられずに、実例を見せてくれと言いました。
そこでソクラテスは、見せてやるから誰か連れてきてみ、と答えて、それに応じてメノンくんはじぶんちの召使いを連れてきます。
この召使い、ギリ言葉は分かりますみたいな設定です。
そんな召使いに、ソクラテスは正方形の面積にまつわる問題を出します。
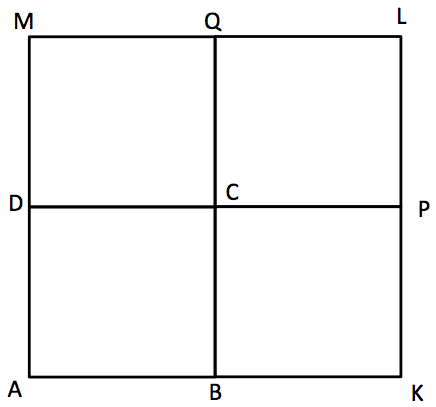
ソクラテスは地面に正方形ABCDを描きます(ギリシアだからホントはαβγδ?)。
ソクラテス 正方形がもっているこれらの線ー四つあるねーは、全部等しいものだね?
AB=BC=CD=DAであることを確認します。これは正方形の条件としては不十分ですが、召使いは同意して次に進みます。
続いて、各辺の中点を結ぶ線(線分)の長さも各辺と等しいことを確認します。
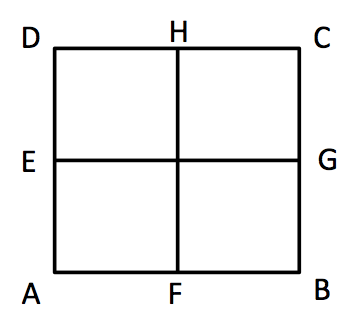
AB=BC=CD=DA=EG=HF、AF=FB、BG=GC、CH=HD、DE=EA。
召使いはこれにも同意します。
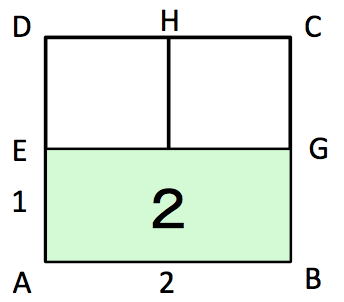
続いて面積を導入します。正方形の各辺の長さは色々な大きさを取れることを確認したうえで、ここではAB=2の場合を考えます。
AB=2なら、AB=DAですからDAも2です。DE=EAより、DA=DE+EA=2EA=2ですから、EA=1です。
ソクラテスはまず、ABGEの面積はAB×EA=2×1で2だと言います。
正方形ABCDは、このABGE二個分の面積だから、2×2で4だと言います。
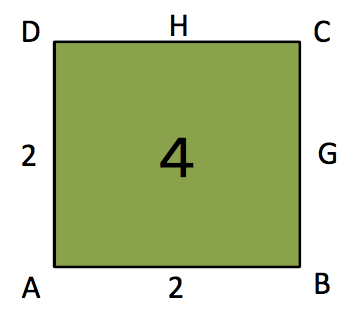
若干まどろっこしいやり方ですが、面積を分割して考えること、また「二個分」という考え方が自明のものであることを確認したのだと思います。
ここまでの内容について召使いは全てわかりきっていることとしてソクラテスに同意します。
もうひとつの正方形
ソクラテスは次に、面積が4と判明した正方形ABCDの二倍の面積を持つような正方形は存在するか、存在するならその面積はいくつか、と召使いに聞きます。
召使いは、そのような正方形は存在し、面積は8だと答えます。
そこで、ソクラテスは召使いに問題を出します。
その図形のひとつひとつの線は、どれだけの長さだろうか。
その図形、というのは面積が8となる正方形のことで、問題はそのような正方形の一辺の長さはどれほどか、ということになります。
正解が2√2であることを中学生以上の読者はすぐに分かると思いますが、召使いは違った答えをだします。
召使いの答え①
ソクラテスに対して、召使いは「むろん」と前置きして、たぶん即答で、正方形ABCDの一辺の二倍の長さ(つまり4)です、と答えます。
そこでソクラテスは一辺が4となる正方形をさきほどの図形に加えて正方形AKLMを描きます。
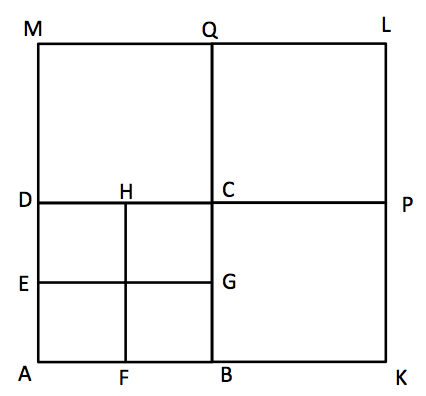
ここで新たに登場した正方形BKPC、CPLQ、DCQMは全て正方形ABCDと同じ面積を持ちます。
よって、AKLMの面積は4×4で16となります。つまり、一辺が4の正方形の面積は、召使いの予想した8ではなく16であることがこの図から分かります。
召使いはこれをみて、面積8の正方形の一辺の長さは4ではなかった、と認めます。
召使いの答え②
そこで召使いは次に、面積が8となる正方形の一辺の長さは、3だと言います。
一辺の長さ2の正方形の二倍の面積を持つのだから、当然2よりは大きかろう。
かといって、一辺が4だと正方形が大きくなりすぎました。
そこで、正解となるのは2より大きく4より小さいはずです。
ソクラテスはそのように召使いに言って、召使いもそれに同意します。
そして、召使いは3が答えですと言います。ソクラテスに誘導された感じはあるものの、あくまで召使いが自分で出した答えです。
さて、一辺が3の正方形は、先ほどの図形でDMの中点とBKの中点から直線を引くことで作図できます。
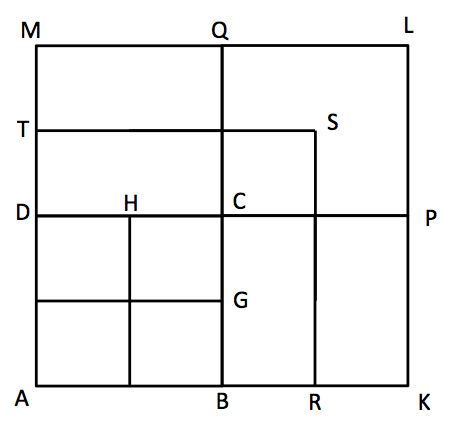
召使いが言った、一辺が3となる正方形は図で正方形ARSTです。
ところが、この正方形ARSTの面積は一辺が3であることから、3×3で9となってしまい、目的である「面積が8となる正方形」ではありません。
面積8の正方形は正方形ARSTより小さく、正方形ABCDより大きいことが分かります。
一辺の長さは、2より大きく3より小さい。
が、召使いはここでお手上げだと言います。
正解
ソクラテスたちは正解を数値としてではなく、図形として示すことを目指しています。
これは『メノン』で特に語られてはいませんが、古代ギリシアでの流儀らしいです。
そこで、ソクラテスも正解を図形で示します。
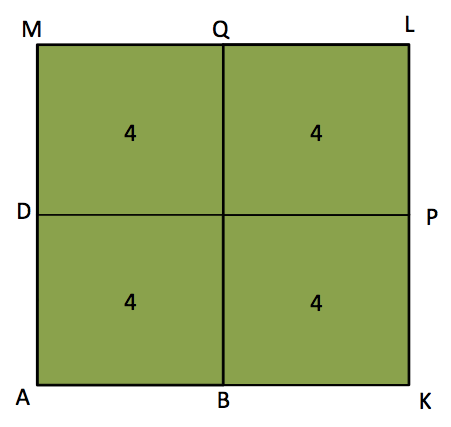
煮詰まってしまった召使いに、ソクラテスは一辺が2の正方形ABCDと、一辺が4の正方形AKLMが重なった図形を再び示します。
召使いの答え①で判明したように、ここにある正方形ABCD、BKPC、CPLQ、DCQMは全て面積が4と等しく、正方形AKLMの面積はABCDの4倍の16です。
よって、求める面積8の正方形というのは、正方形ABCDの二倍であると同時に、正方形AKLMの半分の面積ということになります。
そこで、ソクラテスはAKLMを構成する4つの正方形をそれぞれ半分に分割します・・・対角線を引いて。
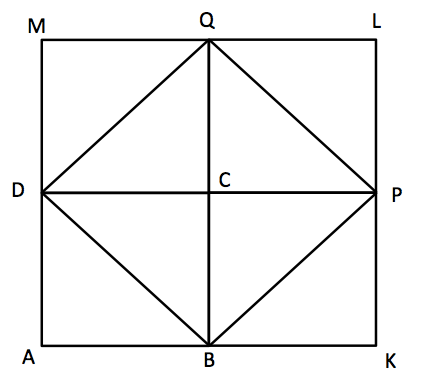
それぞれの対角線DB、BP、PQ、QDは正方形ABCD、BKPC、CPLQ、DCQMを半分に分割しています。
ですから全体としては正方形AKLMを半分に分割しています。
また、それぞれの対角線の長さは同じ大きさの正方形の対角線なので同じです。
よって、四角形DBPQは全ての辺の長さが等しく、また面積が8となります。
この議論は召使いに最初理解されませんでしたが、正方形AKLMを4つの正方形に分割して各々の正方形で議論することで納得されます。
ソクラテス「どやっ(・`ω・)」
これで実例はおしまい。
召使いはお役御免となって、ソクラテスはメノンくんに「どやさ!」ってな感じで鼻息荒く「想起説は正しかっただろ?」と言います。
え?(^ー^;
ただ単に、数学の問題を解いてみただけにしか見えません。
流れをまとめると。
問題:一辺が2の正方形の二倍の面積を持つ正方形の、一辺の長さはいくつか
(一辺が2の正方形の面積は4なので、面積が8となる正方形の一辺の長さ)仮説①:召使い「それは4」
仮説①の検証:ソクラテス(図示して)「一辺が4だとすると、正方形の面積は16」
召使い「ほんとだ。4ではないですね」仮説②:召使い「それは3」
仮説②の検証:ソクラテス(図示して)「一辺が3だとすると、正方形の面積は9」
召使い「ほんとだ。3ではないですね」仮説③:ソクラテス(対角線を図示して)「一辺が2の正方形のこのような線の長さだとどうか」
仮説③の検証:召使い「面積は8ですね、元の正方形の二倍の面積となっていて正しい。」
ソクラテス「これを対角線というんだよ」
ソクラテスは図を書いて、召使いに提案はしたものの、仮説が間違っていること、正解が正しいことの判断は全て召使いが自分で下しました。
これを持ってして、ここでの出来事は「学び」ではなく「想起」だというのです。
フツーに教育の現場で行われる数学の「学び」にしか見えませんが・・・
というわけで、次回。
これのどこが「想起」なのか検討してみます。
あわよくば、僕が勝手に改変した「想起」の方でも意味が通っていることを願いつつ。
息子はさらに盛り上がってDVDを見ていて、『いじわるなハロー』はまだ遠い(;ー;)



