公理を使って導かれる法則が定理。
ということで、公理1から定理を導いてみる・・・のかと思いきや、定理を提示して、それを既に分かっている公理を使って証明する、というのがスタイルのようです。
定理1
相異なる二直線は交わらないか、またはただ一つの点で交わる。
ついつい義務教育での数学の習慣で、二直線の関係を「交わるか平行か」なんて考えてみても「それ以外はありえない」をどう示せばよいのか分かりません。
この証明はもっとずっとシンプルに、公理1に適合するかだけを考えて行われます。
相異なる二直線が、二つ以上の相異なる点で交わっていると仮定するのです。
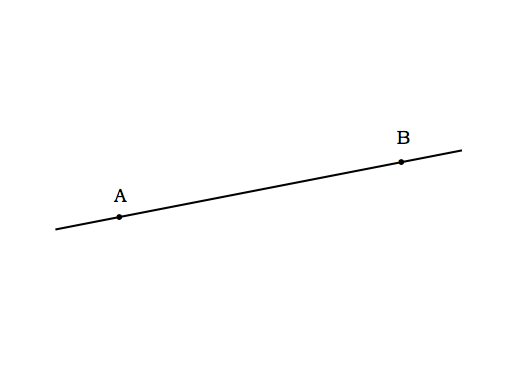
二つ以上の相異なる点で交わるということは、二点A、Bを通る直線が二つ存在することになり、これは公理1に明らかに反してしまいます。
Aを証明するために、A以外はありえないことを証明する、という背理法のパターンです(もっとも、『幾何のおもしろさ』では背理法より帰謬法という呼び方を推奨しています)。
公理を使う証明というのを、僕は初めて体験した気がしました。
やって思ったのは、何ともシンプル。
背理法自体が正しいことの証明はなくていいのかな?と思いましたが、そこ以外は隙の無い完璧な証明に見えます。
「交わるか平行か」という一般常識を公理が密かに支えていたというのも面白いです。
少なくとも僕は、常識に思っていることを何が支えているのか、あんまり意識していなかったと自覚しました。
それにしても、公理を使った証明って、なんか実感が湧きにくいというか、感覚に結びつかないというか、不自然に感じてしまいます。
もっとトレーニングが必要なみたいです(^ー^;